Atualizar o Microsoft Office Starter 2010
Após o lançamento do Office 2010 Starter, a Microsoft buscará mais clientes para migrar do Starter para a versão final ou atualizá-lo. Parece que
Multiplicação de matrizes (MMULT) do Excel 2010
Anteriormente, abordamos como calcular a inversa de uma matriz. Agora, usaremos a função inerente MMULT do Excel para calcular a multiplicação de uma matriz diretamente, em vez de recorrer à formulação manual. Ela também lida com valores de dados como uma matriz e recebe uma matriz como argumento(s).
Abra a planilha do Excel 2010 na qual você precisa descobrir a multiplicação de matrizes. Por exemplo, incluímos uma planilha contendo os campos: Matriz1, Matriz2 e Multiplicação, como mostrado na captura de tela abaixo.
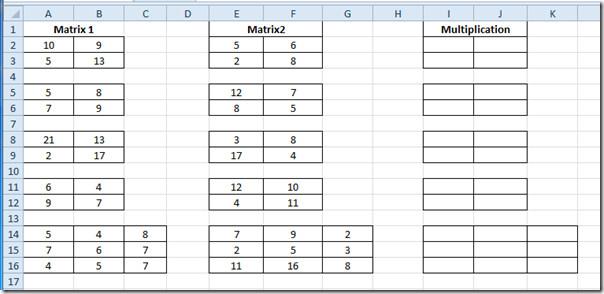
Vamos descobrir a multiplicação das matrizes. Temos três matrizes 2×2 e uma 3×3. A fórmula seria exatamente a mesma para cada categoria. O método antigo de calcular a multiplicação poderia ser muito longo, especialmente quando lidamos com matrizes 3×3. Mas usaremos a função MMULT. A sintaxe básica dessas funções é:
=MMULT(matriz1,matriz2)
O primeiro e o segundo argumentos da função são um array simples, pois recebem array como argumento. Colocaremos a localização da célula onde o array está localizado. No entanto, você também pode inserir valores diretamente.
Escreveremos esta função como;
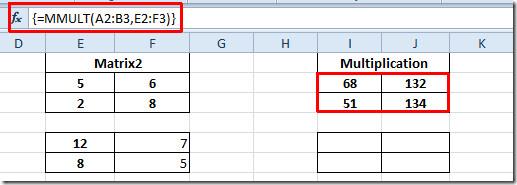
{=MMULT(A2:B3, E2:F3)}
Como A2:B3 é a localização da célula onde reside nossa primeira matriz e E2:F3 é a localização da segunda, como estamos lidando com matrizes aqui, você precisa pressionar Ctrl+Shift+Enter para colocar a função entre chaves, o que indica o uso de matrizes.
Agora, selecione as primeiras células da matriz no campo Multiplicação e insira a função conforme mencionado acima. Isso produzirá o resultado da multiplicação em 4 células, pois calculamos uma matriz 2×2.
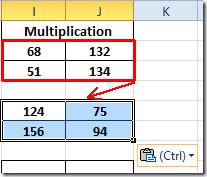
Para descobrir os resultados da multiplicação em outras matrizes, selecione a matriz avaliada e copie e cole em outras matrizes 2 × 2. Como mostrado abaixo, acabamos de copiar a matriz para a matriz abaixo dela.
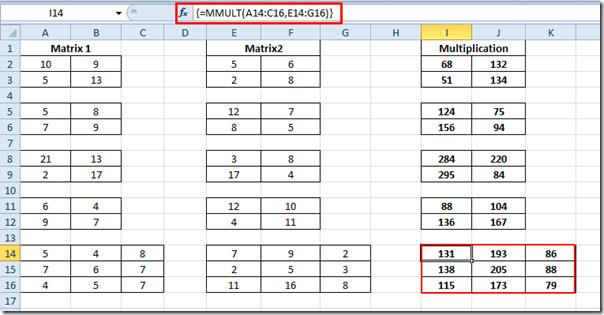
Agora repita o mesmo procedimento para todas as matrizes 2 × 2. Para a matriz 3 × 3, escreva a função novamente, fornecendo a localização de cada célula em ambas as matrizes.
{=MMULT(A14:C16,E14:G16)}
Você também pode conferir a operação de matriz Função revisada anteriormente; Avaliando o determinante da matriz (MDETERM) e Descobrindo o inverso da matriz .
Excel 2010: Função Matriz Inversa (MINVERSE)
Anteriormente, abordamos como avaliar o determinante de uma matriz. Agora, vamos nos concentrar em como encontrar a inversa da matriz, que é principalmente
Correção do MathType no Office Word 2010: Substituir o Editor de Equações
MathType é um complemento bastante popular para o pacote MS Office e é usado por milhares de usuários corporativos. É um poderoso editor de equações que adiciona equações matemáticas
Excel 2010: Alterar a orientação do texto na célula
Muitas vezes, é necessário alterar a orientação do texto em uma célula para ajustá-lo à largura e altura especificadas. A opção Formatar Células oferece uma
Aplicar conjuntos estilísticos de fontes e ligaduras no Word 2010
O Word 2010 contém uma infinidade de famílias de fontes e estilos de fontes, além dos estilos de fontes básicos, ele também inclui alguns estilos de fontes avançados em ligadura
Enviar e receber resultados de pesquisas no Outlook 2010
No ambiente corporativo, é comum receber contribuições sobre diferentes questões em andamento. Embora seja possível coletar respostas sobre questões específicas de várias maneiras,
Inspetor de Documentos do Microsoft Office 2010
O recurso Inspetor de Documentos do Office permite que você verifique se há propriedades ocultas e informações pessoais no seu documento. Como o recurso de coautoria do
Dicas do PowerPoint 2010: Alterar o número padrão do slide
Sempre que você cria uma nova apresentação, o PowerPoint a numera como padrão. Se você estiver trabalhando em uma apresentação maior e outros membros também estiverem envolvidos,
Multiplicação de matrizes (MMULT) do Excel 2010
Anteriormente, abordamos como calcular a inversa de uma matriz. Agora, usaremos a função inerente MMULT do Excel para descobrir a multiplicação de uma matriz.
Alerta de e-mail: Notificação por e-mail para Outlook 2010
A Microsoft surpreendentemente deixou o recurso de notificação no escuro com o Outlook 2010. Existem muitos complementos de terceiros que integram notificações em